Предлагаем в виде самосовершенствования заняться на компьютере делом и занимательным, и вполне серьёзным - моделированием некоторых простейших физических (да и не только физических) явлений. Ведь эта сфера и сейчас остаётся, пожалуй, самой важной и ёмкой областью использования компьютеров. Заведя себе ПЭВМ, было бы просто нелепо не попытаться составить представление о столь важном направлении. Глядишь, удастся оживить и заложенные некогда в глубины мозга сведения из школьной и институтской физики и математики...
Н. ГЕРМАН
ВСЕ - ЗА КОМПЬЮТЕРЫ!
С момента появления в широкой продаже первого отечественного персонального компьютера БК-0010 прошло не так много времени, но уже можно заметить, что спрос на это чудо техники после периода начального ажиотажа заметно упал.
Более всего здесь настораживает активность рекламы, которая у нас выполняет всегда довольно своеобразные функции. Может внушить беспокойство и пустынный зал магазина «Электроника», где два скучающих продавца вечно режутся в игры на БК... А вот оживление у прилавков магазина «Вычислительная техника», где торгуют калькуляторами, никогда не стихает. За рубежом, однако, уже успело прокатиться несколько волн спроса на ПЭВМ.
Уместно поэтому задаться вопросом: для чего вообще необходимы персональные компьютеры (ПЭВМ)? Конечно, если по роду своей профессиональной деятельности вам приходится обращаться к расчётам на ЭВМ, ответ может быть достаточно ясным: теперь, как может показаться, все подобные расчёты можно делать дома.
Ну а если вы не профессиональный математик, физик, программист и т.п.? Попробуйте сообщить своим знакомым, что купили или ещё только намереваетесь купить себе персональный компьютер, и, скорее всего, услышите в ответ: «А какие в нём есть игры?» Итак, ПЭВМ - просто очень сложная игрушка? Что и говорить, компьютеры сумели изрядно преуспеть и в игровом деле. Известно, правда, что в шахматы хороший мастер пересилит самую сложную ЭВМ, но вот, например, в нарды машины уже более десятка лет обыгрывают даже чемпионов мира (существуют и такие). Одним словом, из нашего БК вполне может получиться достойный партнёр, крупье, а возможно, и... шулер. Итак, компьютеризируем домино, очко, лото, преферанс?
Символы карточных мастей на клавиатуре БК говорят о том, что конструкторы не обошли вниманием это важное направление развития человеческого духа. Отметим, что игра, записанная на штатной кассете БК под девизом KOSTI, представляет собой точное воспроизведение известной и до компьютеров игры, где партнёры добывали себе очки именно бросанием костей, что на БК «моделируется» производством случайных (а фактически, как мы скоро убедимся, псевдослучайных) чисел. В качестве курьёза укажем, что в журнале «Радио» (1985, № 6) предлагалось использовать микрокалькулятор для «угадывания» результатов «Спортлото» (также путём генерации случайных чисел). Программа бросания костей на N граней для калькулятора приведена в апрельском выпуске нашей серии (см. Отечественные калькуляторы).
Впрочем, оставим эту тему для отдельного обсуждения.
Так чем же посерьёзнее можно заняться на БК? Пробежимся ещё раз по руководству пользователя и просмотрим рекламный ролик, записанный на штатной кассете БК. Ведение семейного бюджета, регулирование микроклимата и освещённости в квартире, создание собственного банка данных - всё это звучит заманчиво. Итак, заводим этот самый банк. Но вот что в нём хранить? Каталоги коллекций марок? Варианты обмена квартиры? Телефоны знакомых? Досье разве на кого завести? М-да, кое-какие возможности, конечно, вырисовываются. Но нужно прежде всего выяснить, какие преимущества мог бы иметь компьютерный банк, основанный на БК, по сравнению с обычным блокнотом, скоросшивателем или амбарной книгой. Хранимые данные необходимо прежде всего «напечатать», т.е. набрать на клавиатуре БК, затем переписать их на магнитную ленту, а при необходимости прочтения или переработки - перевести обратно с ленты в машину и т.д. Достоинство электронных банков - в возможности быстрого автоматизированного поиска, обработки, перетасовки информации. Если же при этом не организовать автоматизацию всех процессов записи, перемоток и поиска нужных участков ленты на магнитофоне, то практически все мыслимые преимущества нашего банка улетучатся.
Последние модели магнитофонов в принципе позволяют (при доработке) автоматизировать режим перемотки, а некоторые - и ускоренный поиск нужного участка. Дело это, однако, по плечу лишь опытным радиолюбителям. Специализированных магнитофонов, а тем паче дисководов, наиболее приспособленных для хранения данных, в продаже пока нет.
С ними испаряются и надежды на поправку семейного бюджета за счёт БК, поскольку его роль в этом деле реально может свестись разве что к аккуратной записи расходов. Регулировать освещённость и квартирный микроклимат, разумеется, принципиально возможно, но цель здесь вряд ли оправдает затраты интеллектуальных и материальных ресурсов (ведь понадобятся какие-то ЦАП и АЦП и т.п.) да и старые средства - шторы, выключатели и форточка - не кажутся пока безнадёжно устаревшими...
Микросхемы ЦАП и АЦП теперь свободно можно купить в той же «Электронике». Но в целом предлагаемое применение БК кажется малопрактичным и вообще надуманным.
В серии статей, начатой в журнале «Энергия» (1986, № 8), мы предложили новым рекрутам кибернетизации для освоения возможностей БК и в виде самосовершенствования заняться на компьютере делом и занимательным, и вполне серьёзным - моделированием некоторых простейших физических (да и не только физических) явлений.
Дети вот поглядывают на компьютер: игры-играми, но их тоже пора знакомить с существом дела... Словом, вперёд, за моделирование!
С чего же начать в этом направлении? Любая задача, связанная с моделированием какого-либо процесса, явления, всегда может быть разложена на ряд элементарных этапов - от представления нужной информации в привычном виде, нахождения точек пересечения каких-либо зависимостей, т.е. решения линейных или даже трансцендентных уравнений (систем уравнений), до построения решений дифференциальных уравнений в частных производных (это и самая общая форма выражения наиболее фундаментальных законов природы, и самая, пожалуй, трудная в практическом отношении проблема). Обычный путь постижения любой науки - движение от простого к сложному. Этот путь не короток, но нам, конечно же, придётся так или иначе следовать подобному восхождению к сложности. Но начать мы предлагаем ни со сложного, ни с простого, а со случайного.
В кибернетике известен такой тезис: всякий выбор, отличный от случайного, порочен. Автор, выбирая «случайное» начало, руководствовался не этим экстремистским лозунгом, но более рационалистическими соображениями...
Полагаем, что таким путём нам удастся гораздо быстрее окунуться в гущу премудростей моделирования и ощутить кое-какие прелести и ограничения (это не менее важно) компьютера. Вообще это, пожалуй, лучше всего соответствует духу названия всей нашей серии. За рога - так за рога!
Автор имеет в виду рубрику "БК ЗА РОГА", в которой будет рассказано о работе с компьютерами БК-0010 и БК-0011. Статьи этой рубрики см. в последующих выпусках.
Набираем программу:
1.1 S X=128;S Y=128 1.2 X FT(1,X,Y) 1.3 S Х=Х-FRAN(); S Y=Y-FRAN() 1.4 G 1.2
Большая часть распроданных БК понимает ФОКАЛ, и поэтому мы будем печатать программы в этом варианте. Для пользователей БК с БЕЙСИКОМ мы будем указывать смысл операторов, их аналоги и т.п. Перевод наших достаточно простых программ - дело несложное, тем более что оба языка восходят к общему источнику - ФОРТРАНУ. Как мы увидим, ФОКАЛ, представляющий собой как бы предельно упрощённый диалект (своего рода пиджин-инглиш), создаёт своему пользователю определённые удобства: операторы обозначаются всего одной буквой, строки программы можно легко объединять в страницы и т.д. Но разумеется, у более развитого БЕЙСИКа свои серьёзные преимущества.
После её запуска в центре экрана возникает точка, которая хаотически мечется по экрану, зачерчивая за собой причудливую область, заполняющую постепенно всё большую площадь. Какое же физическое явление мы здесь смоделировали? Оказывается, это неплохая модель броуновского движения - хаотического перемещения мелких частиц под действием теплового движения молекул. Явление было случайно подмечено английским ботаником Р. Броуном (теперь бы он был, скорее, Брауном) в 1827 г. при наблюдении пыльцы растений в микроскоп. Это явление изучалось в течение не менее столетия как самим Броуном, так и другими именитыми учёными и сыграло важную роль в окончательном становлении атомистических представлений.
В нашей модели хаотические перемещения частицы задаются особой случайной функцией FRAN(), которая каким-то образом заложена (как говорят ещё, «зашита») в памяти (ПЗУ) БК. Со свойствами нашей функции FRAN и других случайных функций нам ещё предстоит основательно освоиться. Пока же обратим внимание на то, что наблюдателю след частицы, разумеется, не виден. Как его убрать с экрана? Добавим строчку:
1.25 X FT(0,X,Y)
След пропадает, но наша точка теперь принимается мигать, напоминая не броуновскую частицу, а, скорее, порхающего мотылька. Можно попытаться слегка приглушить это мигание:
1.25 X FT(0,A,В) 1.27 S A=X;S B=Y
Идею можно обобщить, что приведёт к ползанию червяка или амёбы длиной К:
1.05 А "К",К 1.10 S Х(K+1)=128; S Y(K+1)=128 1.15 F N=1,K; S X(N)=X(N+1);S Y(N)=4(N+1) 1.20 S X(K+)=X(K+1)+FRAN( );S Y(K+1)=Y(K+1)+FRAN() 1.30 X FT(1,X(K),Y(K)); X FT(0,X(1),Y(1));G 1.15
Оператор F - то же, что FOR БЕЙСИКа, его первый операнд - начальное, последний - конечное значение параметра цикла, средний (если он указан) - шаг цикла. Если его нет, шаг равен единице. Оператору A(ASK) в БЕЙСИКе соответствует INPUT.
Чтобы оценить заслуги классиков науки, попробуем, как это производилось при экспериментальном изучении явления, зарисовать след частицы (он именуется броуновской траекторией), например, наложив на экран кальку. Возможности документальной записи информации с экрана БК и по сию пору остались столь же ограниченными, как и в самом начале его производства. О графопостроителе не приходится и мечтать. Многие любители сопровождают сообщения в печати (см. «Науку и жизнь») о собственных изысканиях фотографиями с экрана, что говорит о готовности предпринять ради любимого дела самые героические усилия. Тем временем по слухам кто-то где-то изобрёл процесс мгновенной съёмки изображения с экрана на некую плёнку, накладываемую непосредственно на экран. Не станем унывать, глядишь, в результате графопостроитель станет вообще ненужным.
Положение точки при этом следует фиксировать через равные интервалы времени. Чтобы не отвлекаться, устроим себе «часы» прямо в углу экрана:
1.35 X FK(0,0); Т %5,Т; S Т=Т+1
Такой счётчик показывает не мировое время, а лишь число «шагов» БК, но пока нам допустимо считать, что он «шагает» равномерно, что, конечно, не совсем точно.
Оператор X FK(X,У) устанавливает начальное положение курсора, откуда и начинается печатание, Число, стоящее за знаком %, определяет полное количество знаков печатаемой величины (целая часть) и количество знаков после запятой (дробная часть).
Чтобы нащупать наиболее благоприятные условия наблюдения броуновских траекторий, можно менять величину элементарного шага частицы.
Предложенное положение центра экрана соответствует укрупнённому масштабу по оси X, более удобному для пользователей с недостаточно острым зрением (увы, и автору). Переключение масштабов производится клавишей 32/64, нажимаемой вместе HP. Код этой команды - 155. Действие клавиш БК понимает даже во время выполнения какой-либо программы. Те же особенности имеет и команда «курсор» (код - 154), включающая и выключающая надоевший мельканием курсор.
Увеличим его, например, в 5 раз (тем самым мы смоделируем переход к большему увеличению в нашем «микроскопе»). Последовательные положения частицы при зарисовках принято соединять отрезками прямых линий (это не означает, конечно, что частица действительно двигалась по прямым). Восстановим след:
1.30 S X=X+5*FRAN(); S Y=Y+5*FRAN() 1.12 X FT(0,X,Y); X FV(1,X,Y)
В таком виде след частицы на экране напоминает результаты непосредственных зарисовок исследователей, которые можно найти хотя бы в БСЭ. Но наш БК позволяет заметно облегчить процесс зарисовки траектории, поскольку вся она сохраняется на экране и её можно срисовать в конце процесса целиком, не гоняясь за самой частицей.
Какие же цели преследовались при подобных зарисовках, на которые пришлось потратить немало терпения и изобретательности? Оказывается, при всей явной запутанности траекторий в них может быть выявлен целый ряд своеобразных статистических закономерностей. С некоторыми из них нам ещё предстоит ознакомиться. Пока же мы предложим нашим читателям несколько упражнений для более основательного знакомства как с самими случайными блужданиями (таково математическое наименование подобных процессов), так и с возможностями нашего премудрого БК. Полагаем, что и сами читатели смогут разработать какие-то свои варианты наблюдения случайных процессов.
- Траектория приближается к краю экрана и, того
гляди, вообще уйдёт за него. Заставьте её «отразиться» от этого (вообще любого)
края, а затем и от любой заданной границы, причём не обязательно прямолинейной.
Не сможете ли вы заставить частицу блуждать внутри какой-либо окружности?
Пока нас мало заботит качество отражающей границы. Ведь частица всегда оказывается от неё на случайном расстоянии. Достаточно, например, такого простого устройства:
1.4 I (Y) 1.5, 1.5, 1.2 1.5 S Y=Y+1;G 1.2
Оператор I это IF и в БЕЙСИКе, но адресация у него иная: первым указывается адрес, куда следует обратиться» если выражение, следующее за I, отрицательно, вторым, если оно равно нулю, затем, если оно положительно. Если адресов не хватает, будет выполняться следующая строка.
- Пусть частица, исчезнув с одного края экрана, «возникнет» с противоположного края (сверху - снизу).
- Выпустите из центра одновременно несколько (две, пять, сто) частиц. Выпустите несколько частиц из разных точек экрана.
- Заставьте ваш БК погонять частицу в течение некоторого
достаточно большого времени (более 40 тыс. шагов). При этом придётся предусмотреть
какие-то меры, чтобы частица действительно не уползла за край экрана, - подобрать
масштаб, может быть, устроить отражающие границы. Поскольку блуждающая точка
часто теряется в уже зачерченных ею областях, можно научить её подмигивать один
или несколько раз на каждом шагу или после определённого числа шагов.
При выполнении любых упражнений, требующих длительного наблюдения, телевизор (после того как вы убедились, что программа начала функционировать нормально) можно использовать по его прямому назначению (во избежание косых взглядов домашних на всю эту кибернетику). Вырабатываемое БК изображение будет при этом храниться в его памяти (ОЗУ).
Подобные длительные «зарисовки» полезно проделать и с несколькими частицами, выпущенными из разных точек экрана (постаравшись, чтобы траектории не перепутывались слишком сильно).
При достаточно большом числе шагов можно будет обнаружить, что в изображаемых фигурах начинает проступать определённая симметрия. Для того чтобы выявить её более наглядно, повернём наши фигуры на 45°. Для этого достаточно откладывать на координатных осях не сами переменные X и У, а значения X - У, и X + У (при этом изменится, правда, и масштаб, но при желании и это можно подправить, введя дополнительный масштабный множитель
).
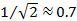Предупредим сразу возможное недоумение наших исследователей: реальная броуновская
траектория, разумеется, не может приобрести никакой симметрии, это было бы слишком
случайно! Наш результат - первое свидетельство неких особенностей процесса генерации
«случайных» чисел внутри БК. - Все предыдущие упражнения можно видоизменить, заставив частицу совершать шаги постоянной (например, единичной) длины вдоль каждой координатной оси. Полезно отметить, как трансформируется вид фигуры, получаемой при большом числе шагов, в этом варианте. Не сохраняется ли всё же определённое сходство?
Ещё одно полезное усложнение - организовать перемещение шагами постоянной длины, но ориентированными случайным образом. Наконец, почему бы не заставить нашу частицу перемещаться не по плоскому экрану (т.е. всего в двух измерениях), но подобно тому, как блуждает реальная броуновская частица, - в трёхмерном пространстве? Ну а в четырёх-, пятимерном? Конечно же, в конце концов результат должен быть поневоле представлен в виде проекции всё на тот же плоский экран, но не возникнут ли при этом какие-то отличия?
Пока компьютер предаётся заданным вычислениям, пользователи получают блестящую возможность поразмышлять на сопутствующие темы (одна из возможных тем о пользе компьютеров, роботов и прочих автоматов как средств, высвобождающих человеку время для размышлений). Подкинем им некоторые сведения из теории случайных блужданий для постепенного осмысления.
Основной закон, который выверялся и при экспериментальном изучении броуновского
движения, заключается в том, что частица в среднем удаляется от любой начальной
точки таким образом, что средний (т.е. усреднённый по множеству независимых
испытаний) квадрат удаления частицы от этой точки растёт пропорционально времени.
Для случая же, когда, как и на экране БК, блуждания осуществляются конечными
дискретными шагами, средний квадрат удаления
оказывается
просто равным
,
где N - число шагов, а
-
средний квадрат длины одного шага. Приведём пример, который может пояснить существо
этого важного закона.
Бросим на пол по возможности наиболее беспорядочным образом N спичек, а затем
сложим все спички по правилам сложения векторов. Какую длину будет иметь результат
такого сложения? Может показаться, что он должен равняться нулю, поскольку все
направления на плоскости равноправны и «результат» просто некуда направить.
Нетрудно представить, однако, что, для того чтобы обратить сумму всех наших
векторов в нуль, придётся как-то весьма специальным образом разложить их на
плоскости. Поэтому какая-то случайная «некомпенсация» всех направлений всегда
образуется, причём в среднем результат (сумма длин спичек как единичных векторов)
будет равен
.
Сами же средние смещения (т.е. вектор результирующего смещения снова усреднённый
по многочисленным испытаниям) должны равняться нулю именно в силу изотропии,
т.е. равноправия всех направлений на плоскости.
«Спичечной» интерпретацией удобно воспользоваться, чтобы самостоятельно доказать основной закон, хотя бы методом математической индукции. Полезно попытаться вычислить и средний квадрат длины одного шага.
Как организовать проверку этого основного закона для моделируемого нами движения?
Самое простое - печатать вслед за показаниями «часов», т.е. числом шагов и квадрат
величины
.
Это стоит проделать хотя бы для того, чтобы убедиться, что вот так просто, на
глазок, никакой вообще связи
и
N заметить невозможно. Дело здесь в том, что любой подобный статистический закон,
утверждающий что-либо о связи средних величин, ещё не вполне полон, пока он
не сопровождается указаниями о допустимых отклонениях от этих средних, или,
выражаясь научным языком, о дисперсии (разбросе) результатов. Так вот оказывается,
что для случайных блужданий по плоскости дисперсия этого самого квадрата удаления
непривычно велика (она просто равна самому среднему значению), что порой ускользает
даже от внимания специалистов. Дабы в этом убедиться, советуем сопроводить блуждания
нашей частицы графиком зависимости
от
Т, для чего придётся подобрать наиболее удобный масштаб, в котором следует откладывать
на осях X и У наши переменные. Обычно для выбора масштаба любой покуда ещё неизвестной
зависимости уважающий себя экспериментатор справляется у знакомого теоретика:
что должно получиться? При этом на осях стараются строить не сами измеряемые
переменные, но какие-то их функции с тем, чтобы ожидаемая теоретическая зависимость
была прямолинейной.
Этот приём весьма полезен, поскольку разглядеть образующуюся из точек прямую очень просто. Наклонив график и посмотрев вдоль прямой, можно немедленно выявить и характер отклонения результатов от «теории», что может дать повод к выявлению причин расхождений. Наконец, наклон прямой и отрезки, которые она отсекает на осях, также можно немедленно сравнить с предсказаниями. Если же получающаяся кривая - именно кривая, то убедиться, что она «правильная» гораздо сложнее.
Мы с вами, уважаемые пользователи, находимся здесь в весьма выгодной позиции:
связь
и
Т известна из теории, и эта связь линейна. Итак, вперёд, за построение графиков!
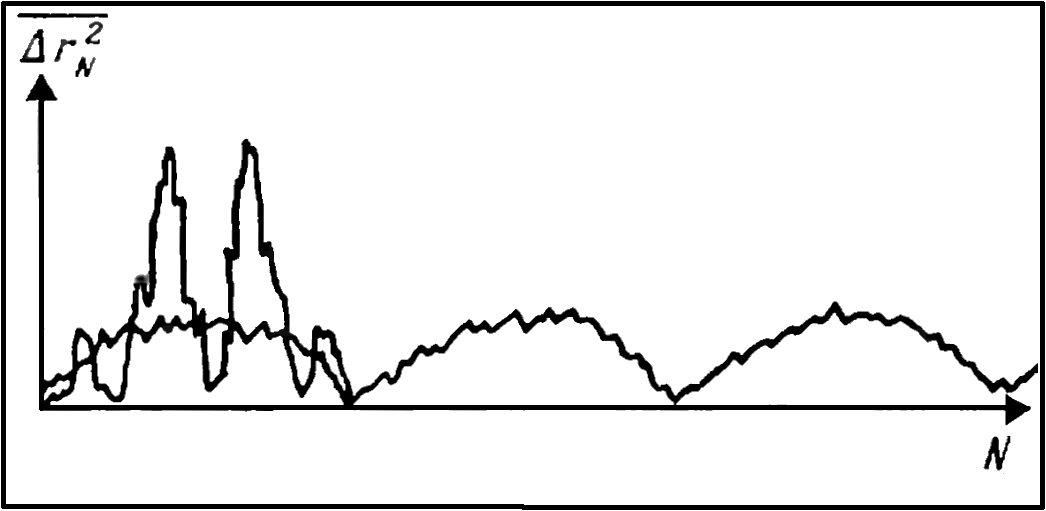
Следует подчеркнуть, что возможность построения различных графиков с помощью БК - необычайно благодарное занятие, и в этом деле пользователь обязан как следует набить себе руку. Правильный подбор масштаба, изображение масштабных меток или сетки, размещение дополнительных надписей, обозначение различных серий экспериментальных точек и т.д. - вот направления неограниченных возможностей совершенствования. На нашем графике можно будет найти место и для изображения самой траектории, но его можно и изъять, если необходимо добиться максимальной скорости изысканий. Дело в том, что нелишне наш график продолжить и до 100 тыс. шагов. Для этого можно заставить БК поработать всю ночь, ведь ЭВМ не нуждается во сне. Единственно, за чем нужно при этом проследить, это чтобы ни БК, ни его источник питания не были завалены бумагами, а находились бы на открытом месте. Надеемся, что, вскочив утром в радостном волнении истинного исследователя и включив телевизор (именно его, пожалуй, и не следует держать включённым всю ночь), вы обнаружите, что ожидаемая теоретическая прямолинейная зависимость... не выполняется. Что же это такое? Снова шутки дисперсии?!
Дисперсия, конечно, дисперсией, но с ней, оказывается, можно побороться.
Наиболее дотошные читатели могут даже по этому поводу вычислить дисперсию квадрата
удаления и обнаружить, что... в пространстве размерности К нормированное
значение дисперсии равно
.
Самое интересное, пожалуй, в том, что эта величина не зависит от числа шагов.
Поэтому обычные в статистике надежды на то, что чем больше шагов, тем лучше
всё получается, в данном случае не работают. Увеличивать надо не число шагов,
а размерность пространства.
Мы не случайно уже предлагали нашим пользователям поупражняться в блужданиях в многомерных пространствах. Нетрудно сообразить, что каждое последовательное обращение к функции FRAN вполне эквивалентно невидимому шагу в неком невидимом измерении. Просуммировать же квадраты смещений по всем двумстам измерениям для БК - сущий пустяк.
Нетрудно сообразить, что запуск большого числа частиц и суммирование (непосредственное или просто графическое - путём наблюдения за площадью, зачерчиваемой всеми частицами) квадратов их удалений также соответствуют увеличению размерности броуновского пространства. Можно использовать и одну-единственную плоскую траекторию, суммируя квадраты удаления не от одной исходной, а от большого количества последовательных точек. Этими приёмами можно основательно сгладить первоначальную довольно корявую кривую.
Зато дисперсия в таком пространстве составит всего 10%, и отклониться теперь от ожидаемой прямой заметным образом наши результаты не должны... Не должны-то не должны, а вдруг? Но оставим на этом месте самых дотошных читателей, если они пожелают ещё глубже ознакомиться с особенностями случайных блужданий. Предложим им напоследок такую вот тему для самостоятельного исследования: можно ли на БК продемонстрировать, что основной закон случайных блужданий выполняется с точностью, с которой он был экспериментально проверен для случая броуновского движения, т.е. в несколько процентов? Здесь снова придётся поразмышлять над терпением классиков науки.
Именно путём обработки броуновских траекторий было впервые измерено значение постоянной Больцмана к, а через него и число Авогадро N=R/k (R - газовая постоянная), т.е. вес атома. Рекордная для своего времени точность определения была достигнута при наблюдении броуновского движения крутильного маятника, фиксировавшегося, правда, киносъёмкой.
Нам же настала пора более пристально приглядеться к свойствам нашей случайной функции - у нас уже были основания заподозрить, что с нею что-то не так... Что же именно? Давайте для начала проверим, действительно ли FRAN производит случайные числа, равномерно распределённые в интервале (-1, +1). Для этого предлагаем построить такую гистограмму:
1.1 F М=1,50; X FT(1,Х(М),Y*M+25); S A=25*(FRAN()+1); S X(A)=X(A)+1 1.2 G1.1
Здесь мы разделили весь рабочий интервал на 50 частей. При попадании очередного случайного числа в какой-либо интервал высота соответствующей клеточки гистограммы (а гистограмма - это «клеточный» график) увеличивается на единицу. Со временем, правда, возникнет опасность, что клеточки выползут за край экрана. Можно поэтому построить зависимость величины реального заполнения каждого интервала от ожидаемого (среднего) значения:
1.1 F М=1,50; X FT(1,X(M)*128/(T+1),25+Y*M) и т.д. 1.2 X FCHR(12); X FK(0,0); Т Т; S T=T+1; G 1.1
Проследите, как меняется разброс (дисперсия!) от среднего заполнения при увеличении количества чисел. Хорошая случайная последовательность должна обеспечивать не только равномерность заполнения рабочего интервала, но непременно и соответствие дисперсии заполнения своему теоретическому значению. Напомним (а это один из самых важных и наиболее практически популярный результат теории вероятностей), что для малых интервалов при среднем заполнении интервала дисперсия заполнения равна
Распределение отклонений от среднего N при больших N стремится к известной функции Гаусса:
P(N) = ехр(-(N-
)2/(22).
Такое распределение называется нормальным, а приведённое утверждение преподносится
как выражение закона больших чисел. Если попытаться проверить выполнимость этого
закона для FRAN, то может возникнуть проблема правильной нормировки функции
Гаусса. Укажем, что интеграл по N от -∞ до +∞ от приведённого выражения равен
2
.
Подумайте, как организовать количественную проверку и этого обстоятельства, причём здесь также интересно проследить за ходом дисперсии при очень большом случайном числе (более 40 000). Стоит поварьировать и число первоначальных малых интервалов. При некотором минимуме терпения и наблюдательности здесь также можно наткнуться на определённые сюрпризы, достойные последующего осмысления.
Правильное заполнение рабочего интервала - вовсе не единственное требование, которому должна удовлетворять хорошая случайная последовательность. Необходимо также, чтобы последовательные случайные числа, взятые попарно, также были взаимно случайными. Не станем уточнять, как это можно строго сформулировать, а вместо этого проверим нашу функцию FRAN на такие «парные корреляции».
Разбросаем по плоскости X, Y точки, выбирая их координаты, как последовательные пары в нашей случайной последовательности:
3.1 X FT(1,128*(FRAN()+1),128*(FRAN()+1)) 3.2 G 3.1
Смеем вас заверить, что если в самом начале образующаяся карта «звёздного неба» ещё будет поражать (или радовать - это уже дело вкуса) именно своей явной хаотичностью, очень скоро в ней начнёт проступать подозрительная упорядоченность, переходящая постепенно в самый строгий порядок.
Сказанное относится к ФОКАЛу, но что именно получится с БЕЙСИКОМ, автор ещё не видел.
Вот тебе и на! Ай да случайность! Какое-то гегелевское единство с необходимостью...
Впрочем, Гегель с его премудростью здесь ни при чём. Но может быть, дело именно в том, что мы взяли именно пары чисел и набросали их на плоскость? Снова бы попытаться окунуться в многомерность... Как её сейчас смоделировать? Полезно опять представить, что и здесь каждое (даже холостое) обращение к FRAN эквивалентно экскурсу в «невидимое» измерение. Итак, приглашаем читателя, вставляя между нашими отстраиваемыми на дисплее парами координат несколько холостых FRAN в разных сочетаниях, попытаться добиться максимума беспорядка.
Упорядоченность в трёхмерном пространстве можно наглядно выявить, если организовать косоугольную (а можно и перспективную) проекцию трёхмерного пространства на экран. Это полезное упражнение может понадобиться по огромному числу поводов! Советуем исследовать «случайные небеса» с большим разрешением (увеличением «телескопа»),
Думаем, что тот или иной характер упорядоченности довольно скоро проступит, что охладит и эти «многомерные» ожидания. Итак, наша «случайность» упорядочена?
Присмотримся же ещё раз к нашей исходной броуновской траектории, получаемой при очень большом (около 30 000) числе шагов. Не знаю, что строит при этом ваш БК, а мой всегда, т.е. независимо от того, где начнётся «рисование», изображает одну и ту же достаточно диковинную фигуру, напоминающую летящее двукрылое (мы уже намекали на определённую симметрию) существо с когтистыми лапами, но без... головы! Мы предложили назвать это дикое создание фантазии БК «демоном». Видимо большинство читательских БК также изображают этого самого демона - есть основания думать, что по крайней мере в определённой серии машин все случайные последовательности просто совпадают. Но ведь в руководстве пользователя написано, что «FRAN... выдаёт... непредсказуемую последовательность случайных чисел!» Впрочем, упрекнуть создателей БК и его программного обеспечения нам здесь не в чём. Разве что авторы руководства, чуть-чуть увлёкшись достоинствами этого произведения человеческого гения (мы имеем в виду именно БК), выразились не совсем точно. Но такое вполне простительно...
Если характеризовать существо программный принципов, на которых основана работа компьютеров, то сделать это лучше одного из наших крупнейших специалистов - академика С. В. Лебедева, по мнению автора, трудно. На лекции, прочитанной в МФТИ на заре компьютеризации в 1954 г., на которой посчастливилось присутствовать и автору, академик на вопрос: «Может, ли ЭВМ думать?», ответил твёрдым «нет» и пояснил: «Машина... ведь она работает, как дура!» При этом имелась в виду сохраняющаяся по сию пору железная детерминированность программ работы ЭВМ. Для генерации случайных чисел компьютер в принципе может использовать и не программные средства, но так называемые физические задатчики (радиотехнический вариант, см. «Радио», № 3, 1987, с. 22). Для таких устройств проблемы обеспечения «правильной случайности», быстродействия и т.п. отнюдь не просты. Сейчас миниатюризация элементов ЭВМ довела их до весьма критической черты: в них возникли «истинно случайные» сбои (наводки, поломки и отказы - не в счёт), вызываемые перезарядкой измельчавших конденсаторов, хранящих биты информации, под действием радиоактивных распадов и космических частиц. Не станем углубляться в обсуждение вопроса, не ускорят ли этот шум и иные случайности дорогу к столь желанному для некоторых искусственному разуму. Подчеркнём только, что упомянутое гегелевское соответствие случайного и необходимого приобретает в этой связи и для компьютеров нетривиальный - квантовомеханический(!) оттенок...
Вообще оказывается, что любой компьютер, пусть самый наимощнейший, если только он работает на тех же физических и программных принципах, что и БК (а пока почти все компьютеры так и работают), даже в принципе не может выдавать непредсказуемую последовательность случайных чисел. Компьютер не может даже выдать вот такую простую и вовсе не случайную последовательность: 10 100 1000 10000 100000 1000000 1000000001 и т.д.
Оба замысловатых с виду утверждения немедленно следуют из простого положения: число состояний устройства из конечного числа элементов, каждый из которых может находиться в конечном числе состояний, также конечно.
Что же касается случайных последовательностей, то рано или поздно любая компьютерная последовательность начинает повторяться. Обычно в качестве самого первого (но далеко не исчерпывающего) критерия качества таких последовательностей указывается именно значение периода, т.е. полного количества чисел, после выдачи которого последовательность начинает строго повторяться. Предлагаем нашим пользователям самим найти значение периода FRAN. Мы уже намекали, что оно должно составлять что-то около нескольких десятков тысяч.
Для дальнейшего нам может понадобиться совершенно точное значение периода.
Если же кому-либо покажется, что найденный период слишком мал, отметим, что в БК действует 16-разрядный микропроцессор, а 216=65536, и это есть вообще максимальное количество различных целых чисел, которые способны в нём возникать. Поэтому не так уж плохо иметь десятки тысяч различных случайных чисел, да и немудрено, что они рано или поздно начинают проявлять какую-то упорядоченность.
Всё же отметить, что наша FRAN начинает когда-то повторяться, значит сказать ещё далеко не всё об её хитросплетениях. Другая особенность, которую нелишне отметить, состоит в том, что демон - фигура замкнутая, а уж если быть вполне точным - почти замкнутая.
Поэтому при проходах нескольких периодов FRAN броуновской частицей демон почти строго начинает «повторяться», но всё же не точно, а с очень малым сдвигом (при паре проходов этот сдвиг можно и не засечь). Предлагаем самим придумать тест для определения точности, с которой последовательные демоны ложатся друг на друга.
Интересно, что на моём БК результат был разным в зависимости от того, производилось ли суммирование всей последовательности или вычитание (набрать на БК минус не в пример легче, чем плюс, который надо давить одновременно с HP, причём именно давить). Исследование выявило «странно-случайное» число, номер которого, считая от начала FRAN (устанавливающегося после включения в сеть), равен 51. Хотя оно равно вроде бы -1, если его вычесть из самого себя, получится не нуль, а -2. Подозрения в нечистоплотности моего БК рассеялись после обследования другого экземпляра. А что происходит с вашим № 51 ?
Отмеченные здесь особенности функции FRAN приведут к появлению ряда своеобразных
отклонений от теоретически ожидаемых статистических законов, в частности и,
в основном законе блужданий. Возврат траектории в исходную точку (на плоскости)
проявится в неоправданном статистически «занулении» зависимости
,
которая, как мы отметили, может быть основательно приглажена. Не вполне же точное
возвращение приведёт к тому, что при большом количестве повторных проходов (строго
говоря, не следует вообще пользоваться случайной функцией, обращаясь к ней большее
число раз, чем значение её периода) пропорционально времени начнёт расти уже
не квадрат удаления, а сама первая степень расстояния. В пространствах большей
размерности, иначе в случаях, когда между двумя фиксируемыми шагами частицы
обращениями к FRAN вставляется несколько холостых (или, если эта функция используется
для каких-либо иных целей), траектория может и не вернуться в исходную точку,
т.е. соответствующий демон не замкнётся. Тогда переход к этому «неправильному»
закону смещения может выявиться гораздо раньше. Уверены, что читатели, запускавшие
на БК по нескольку частиц, успели заметить некоторые указанные нами особенности.
Всё же, сколь нам может и не стать обидно, что коварный БК не столь хорошо соблюдает таинственные вероятностные законы, наше дело представить, где ещё и каким образом это обстоятельство может сказаться в нашем дальнейшем общении с компьютером. Ну вот, например, теперь ясно, что он не может выставить в игре против нас более десятка тысяч вариантов, но для среднестатистического игрока такое количество может считаться приемлемым. Однако снова повторим, что игры - это не наша епархия... А в математике?
Оговорка о среднестатистичности сделана с тем, чтобы подчеркнуть, что люди с исключительными способностями в состоянии запомнить и не такие количества данных. Для профессиональных шулеров и любителей «очка», «железки» и других малопочтенных игр это просто вопрос квалификации. А выдающиеся шахматисты? Легенды, в изобилии ходящие о причудах чемпионов мира, утверждают, что один из них, ныне покойный, после нескольких сдач безошибочно запоминал рубашки всех карт, так что дальнейшее сражение в преферанс становилось небезопасным. Известно, что следует говорить о покойных, но думаем, что подобное исключительное качество и чемпиона характеризует положительно... Игра, «заряженная» в только что включённый в сеть БК, всегда начинается с одного и того же варианта. Полезно вводить в неё несколько предварительных обращений к FRAN, число которых определяется какими-либо случайными действиями игроков, их именами и т.п.
Мы с вами уже производили проверку FRAN на правильность заполнения квадрата. Как и для исходного отрезка, такое заполнение должно быть по крайней мере более или менее равномерным, т.е. в равные по площади части квадрата должно рассеяться в среднем одинаковое число звёздочек.
Это обстоятельство часто используется для нахождения площадей различных фигур, т.е. для вычисления интегралов. Набросаем в квадрат n случайных звёздочек, подсчитаем, сколько попало внутрь исследуемой фигуры, разделим результат на N и найдём грубо требуемую площадь.
Все методы, использующие законы случая, получили обобщающее название методов Монте-Карло. В учёном собрании теперь можно услышать: «Вон идёт известный монтекарлист!» Название произведено от места дислокации некогда наимоднейшего казино с его рулеткой - символом случайности.
Применим этот метод к вычислению площади круга, которая, правда, теперь и
без того настолько хорошо известна, что даже поэт сказал: «
есть
площадь круга!» Поэты же, как все знают, никогда не отличались пристрастием
к точным наукам.
И вот один поэт договорился до утверждения (теоремы): «Площадь круга, площадь круга, два пи эр!» Там, правда, упоминается некая дама из АПН, с которой поэт не прочь познакомиться... Может, это всё его и сбило. Но такое неевклидово решение проблемы квадратуры заметил неутомимый А. Иванов, который не упустил и по сему поводу создать блестящий едкий опус. Эта геометрическая дискуссия лишь добавила вящей славы и без того славному поэту да и самому А. Иванову...
Но тем не менее:
4.1 I ((FRAN())^2+(FRAN())^2)-1) 4.3 4.2 S A=A+1; S P=4*B/A; X FK(0,0); T P,A; G 4.1 4.3 S B=B+1; G 4.2
Как и в большинстве чисто вычислительных задач, нас в этом примере обязан волновать вопрос о производительности ЭВМ, т.е. о времени, необходимом для вычисления числа пи с определённой точностью. Постарайтесь определить, в состоянии ли БК, пользуясь предложенной простой программой, найти пи с точностью лучшей, чем в старинном приближении 22/7? Можно ли добиться существенного улучшения точности и какие меры для этого понадобятся? А как с затратами времени?
Для дальнейшего знакомства с возможностями вероятностных методов вычислений на БК можем также предложить естественно напрашивающееся обобщение нашей задачи на случай трёхмерной, а затем и n-мерной сферы (гиперсферы). Кстати, если для шара ответ все обязаны знать, то для n измерений нелишне будет попытаться как-то найти результат хотя бы по справочникам, а возможно, и непосредственным расчётом.
Число лишних знаков, добытых в числе Архимеда (термин из руководства пользователя), давно стало символом производительности ЭВМ и мастерства программистов. Хотя математика учит, что в записи этого числа в силу его трансцендентности можно в скрытом виде найти все мыслимые сведения и законы, мы не станем тягаться с профессионалами. Мой БК, прожевав всю FRAN, не добыл методом Монте-Карло и трёх правильных знаков. Как ваши БК? (См. также задачу в конце этой статьи). Дальнейшие обобщения: найти моменты инерции фигур, тел, гипертел...
Кстати, если уж затронут вопрос о производительности, его пора начать исследовать экспериментально. Скажем, сколько времени нужно БК, чтобы выдать очередное случайное число? Чтобы ответить на этот вопрос, придётся засечь время, необходимое для совершения примерно 1000 однородных операций (организовав соответствующий цикл), из которых в одном случае все содержат обращение к FRAN, а в другом - нет. Таким путём можно оценить, что необходимо примерно 5мс. Этот результат следует всегда иметь в виду, в частности, при любых попытках «улучшить» FRAN, дополнительно его перетасовать, создать конкурирующую программу или даже внешний «физический задатчик». Полезно аналогичные исследования провести и для других функций, которыми владеет БК, - FSIN, FEXP и т.д.
Однако не станем слишком отвлекаться от намеченного генерального направления и вернёмся к нашей броуновской частице. Добавим к смещению по координате Y (строка 1.3) на каждом шагу небольшую постоянную добавку (0.01, 0.1, 0.5). Запустите видоизменённую программу. Что за процесс она теперь моделирует? Измените знак добавки. Какой объект в природе может изображаться теперь нашей точкой? Устроим из верхней границы экрана непроницаемую (отражающую) преграду и понаблюдаем за нашей частицей некоторое время. Что же это всё-таки за частица?
Постоянное на каждом шагу смещение моделирует движение с постоянной скоростью, которая характерна для движения в вязкой среде под действием постоянной силы (в отличие от постоянного ускорения для свободной частицы). В зависимости от соотношения величины этой добавки со средним броуновским шагом характер результирующей траектории может заметно различаться. Напомним, что в молекулярной физике движение в вязкой среде под действием внешней силы на фоне случайных блужданий называется дрейфом. Если частица дрейфует в какой-либо жидкости вниз под действием силы тяжести, соответствующий процесс называется осаждением, седиментацией (это одно и то же) или даже отмучиванием. Всплывающая же вверх под действием архимедовой силы (она несколько больше веса) капелька жира в молоке участвует в процессе сепарации, приводящем к отделению сливок.
Эти процессы находят важное практическое применение всюду, где нужно что-либо разделить по плотности, размерам. Сепарация молока - серьёзнейшее дело, для него приспосабливалась и центрифуга, и паровая турбина. Фирма, основанная некогда Лавалем, продолжает совершенствовать и это «сливочное» направление, выпускает массу и других быстровращающихся изделий до газотурбинных двигателей и т.п.
Явление дрейфового движения характерно и для некоторых других физических систем. Так, электроны, движущиеся в обычных проводниках, перенося столь важные для нас токи, также дрейфуют, причём для них броуновская, хаотическая составляющая движения гораздо сильнее выражена, нежели направленная. Легко прикинуть, что средние дрейфовые скорости электронов в обычной меди не превышают 1 мм/с, тогда как тепловые скорости порядка 106 м/с. Пусть читатель припомнит какие-либо иные примеры...
На этом мы можем пока прервать наше предварительное знакомство со сферой случайного с помощью БК. В дальнейшем мы ещё не раз будем обращаться к нашей FRAN и как чистые потребители, и как исследователи, поскольку нас не может не интересовать сам процесс производства случайных чисел. Для того чтобы читатель мог хотя бы в самых общих чертах представить, насколько это в целом дело непростое, мы можем порекомендовать ему самым поверхностным образом пробежать взглядом профессиональное исследование (см.: Добрис Г.В. Генерация псевдослучайных чисел и статистические испытания // Программирование. - 1986. - № 2).
Наконец, порекомендуем ещё пару тем, связанных с исследованием случайного, которым и читатель также смог бы заняться самостоятельно (обе навеяны перелистыванием раздела «Занимательный компьютер» из журнала «Жизнь науки»).
- На дощатый пол беспорядочно высыпается множество спичек. Ширина доски равна двум длинам спички. Какой будет доля спичек, пересекающих щели между досками (задача Бюффона, который говорил, правда, об иголках)? Не станем подсказывать ожидаемый теоретический результат. Посмотрим, что легче окажется читателю: найти этот результат именно теоретически или «в машинном эксперименте» на БК.
- Постройте на БК модель известной доски Гальтона, представляющей набор рядов гвоздиков или колышков, на каждом из которых падающий сверху шарик может с равной вероятностью отклониться либо влево, либо вправо. Не будем пока приводить других подробностей устройства доски, предоставив простор конструкторской мысли наших пользователей. Результат каждого столкновения БК может найти просто по знаку очередного случайного числа. Заметим, что распределение шариков по ячейкам доски теоретически пропорционально биноминальным коэффициентам и при большом числе рядов оно стремится к функции Гаусса (это, собственно, и называется законом больших чисел). Предлагаем подумать, как наилучшим образом организовать сравнение результатов с этой функцией.
Приятных случайных блужданий!