А. А. Самбиев
МИНИМИЗАЦИЯ ПРОГРАММ
Структурное программирование имеет массу достоинств, о которых много написано в литературе. Но зачастую программист не может воспользоваться этими преимуществами по той простой причине, что компьютер, с которым он работает, не поддерживает таких возможностей. И если о том, как разработать программу на структурном языке написано много, то для разработки структуры программы на неструктурном языке существуют только блок-схемы. Пока нет методологии, воспользовавшись которой можно было бы однозначно перейти от блок-схемы к программе. Поэтому блок-схемы используются редко, а переход от блок-схемы к тексту программы вызывает новые ошибки и потери времени. В то же время только благодаря рациональной организации условных и безусловных переходов зачастую удаётся значительно сократить объём программы и сделать её текст более удобочитаемым, что особенно важно, если в программе для уменьшения объёма и повышения быстродействия применяются всевозможные «хитрости». И если даже у пользователей компьютеров более мощных, чем БК, часто возникают проблемы, связанные с нехваткой ресурсов, то на БК для решения мало-мальски серьёзной задачи минимизация программы жизненно необходима.
Предлагаемый метод появился в результате длительной работы с языком ЯМБ компьютера «Искра-1256» и служит дополнением к методу блок-схем. Он позволяет однозначно перейти от блок-схемы к тексту программы и может быть легко модернизирован с учётом особенностей конкретного неструктурного языка программирования. Наибольший эффект метод даёт при применении на самой ранней стадии разработки программы. (Стандартная методика составления блок-схем здесь не рассматривается, так как предполагается, что читатель с нею уже знаком. Кроме того, описание начальных этапов разработки программы имеется в литературе. Отметим лишь, что надо постараться получить как можно более простую и короткую блок-схему, тогда и текст программы будет более оптимален.)
Рассмотрим простейший вариант. Пусть мы имеем некий язык, допускающий не более одного оператора в одной строке текста программы; в данном языке имеется условный оператор без альтернативы, причём по условию возможен только переход и только по объявленной метке (таков, например, язык ЯМБ).
Составим программу, реализующую следующую последовательность действий:
|
ЕСЛИ a>b |
|
|
|
с = а+b |
|
|
d = e*f |
|
|
g = h/i |
|
ИНАЧЕ |
|
|
|
с = a+b |
|
|
d = e/f |
|
|
g = h/i |
|
КНЦ |
|
Соответствующая блок-схема будет выглядеть так, как изображено на рис. 1.

Рис. 1
Как видно из блок-схемы, первые и последние операторы в ветвях альтернативы одинаковы. Если первые операторы одинаковы, их можно вынести из альтернативы и поставить до неё. Если одинаковы последние операторы, их можно поставить после альтернативы. В результате мы сэкономим два оператора, и блок-схема примет следующий вид:

Рис. 2
Операторы в программе расположены последовательно, точно так же надо расположить элементы блок-схемы. Проведём на бумаге вертикальную линию и расположим все элементы блок-схемы вдоль неё, не нарушая при этом порядка соединений блоков между собой. Кроме того, необходимо, чтобы в операторе условного перехода он выполнялся при выполнении условия. Иногда для этого необходимо изменить условие альтернативы. В полученной блок-схеме пометим метками те места программы, куда осуществляется передача управления. В нашей программе таких точек две. Удобно размещать метки в порядке возрастания номеров, в алфавитном или любом другом естественном порядке, тогда их легче будет искать. Если же язык требует нумеровать строки, пронумеруйте блоки блок-схемы в порядке возрастания номеров с требуемым шагом. Теперь осталось рядом с элементами блок-схемы написать соответствующие им операторы:
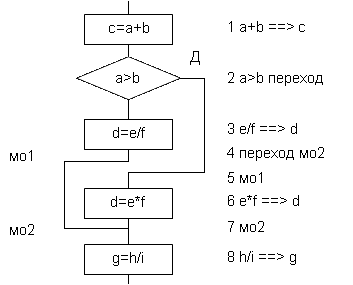
Рис. 3. Программа написана на языке ЯМБ, но для облегчения понимания имена переменных английские, ЯМБ таких не допускает
Программа готова. Конечно, она достаточно тривиальна, но это только пример. Как уже говорилось, метод легко модернизируется в соответствии с особенностями конкретного языка. Например, на Бейсике-БК конструкция должна рассматриваться как один оператор, а так как нет необходимости явно определять метки, то переход надо указывать по номеру строки.
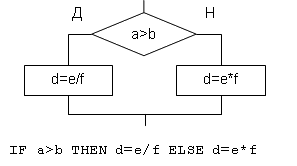
Рис. 4
При большом количестве строк программы можно получить заметный выигрыш в размерах конечного продукта. Причём уменьшение объёма программы происходит не в ущерб понятности и скорости её исполнения, напротив, программа читается легче, а скорость не только не уменьшается, а в ряде случаев заметно возрастает. В частности, более рациональное использование переходов позволило уменьшить размеры программы «Остров сокровищ», опубликованной в журнале «Вычислительная техника и её применение», 1990, №3, с 222 строк до 180 (прим.gid: как обычно, все всё перепутали, в журнале ВТ и её П 1990 №03 опубликована игра "Лабиринт", для БК, а игра "Остров сокровищ" была опубликована в ВТ и её П 1988 №03. Это программа на диалекте бейсика для Искры-1256, поэтому не распознавалась.). Если вы хорошо потрудились над алгоритмом программы, то можете быть уверены, что построить программу с меньшим числом переходов не удастся никому.
В заключение несколько замечаний по программированию на Бейсике. Существует интересная возможность включать в математические формулы логические выражения. Почему-то эта возможность используется крайне редко, хотя её применение может сделать программу более лаконичной, хотя и менее «читабельной».
Пусть надо запрограммировать следующую функцию:
если O% = 1 то J% = 2 если O% = 2 то J% = 8 если O% = 3 то J% = 10 если O% = 4 то J% = 16
Часто в таких случаях пишут
IF O% = 1 THEN J% = 2 IF О% = 2 THEN J% = 8 IF O% = 3 THEN J% = 10 IF O% = 4 THEN J% = 16
или так
100 ON O% GOTO 110,130,150,170 110 J% =2 120 GOTO 200 130 J% = 8 140 GOTO 200 150 J% = 10 160 GOTO 200 170 J% = 16 200 .....
А всё это можно записать од ной строкой:
J% = 2+(O%-1)*6+4*(O%=2)
Дело в том, что при выполнении условия, записанного последней паре скобок формулы, выражение в скобках принимает значение -1, иначе это значение равно 0. Разумеется, такая запись не так наглядна, как две предыдущие, зато коротка.
Разработать обобщённый метод применения этого приёма мне не удалось. Может, это удастся читателям? Я же могу предложить раскладывать такие функции на ряд слагаемых:
J% = слагаемое1+слагаемое2+.....+слагаемоеk.
Каждое из этих слагаемых должно содержать логические условия так, чтобы все слагаемые, кроме одного, обращались в ноль. Затем эту формулу можно упростить, пользуясь правилами математики
Так, ранее рассмотренную задачу можно решить иначе:
J% = VAL(MID$(" 2 81016", O%*2-1,2))
или так:
A$=CHR$(2)+CHR$(8)+CHR$(10)+CHR$(16) J%=ASC(MID$(A$, O%, 1))
- Ужимайте программу как можно сильнее, даже если для её работы не требуется много памяти. Короткая программа быстрее загружается, и уменьшается вероятность ошибок чтения.
- Избегайте обращения к строкам-комментариям. При ужимании программы вы можете удалить комментарий и нарушить работоспособность программы («нет строки с данным номером»).
- Если порядок выполнения операторов не имеет значения, то располагайте рядом «однородные» операторы, например CLS, LOCATE, INPUT, PRINT. Это облегчит чтение программы.
- Избегайте имён переменных, содержащих символы I (латинское заглавное «И»), l (латинское строчное «L»), 1 («один»), Z (заглавное «Зет»), 2 («два»), 0 («ноль»), О (заглавная буква «О») и т.п. Это приводит к ошибкам, которые трудно обнаружить, особенно в случае рукописного текста.
- Если программа требует много памяти, вставьте в неё строку PRINT FRE(""),FRE(0). Это позволит оперативно определять последствия вносимых изменений. (Ещё проще и экономнее время от времени задавать подобную строку на выполнение в непосредственном режиме, не засоряя текст самой программы - Прим peg)
- Пусть есть некая подпрограмма
100 ' подпрограмма ............ 150 GOSUB 200 160 RETURN
В такой подпрограмме, где последним оператором перед RETURN является GOSUB, можно заменить две последние строки на одну:
100 ' подпрограмма ............ 150 GOTO 200
Это позволяет экономить память и немного повысить быстродействие
- Ещё один полезный приём
- вместо
IF X<0 GOTO 100 IF X=0 GOTO 200 IF X>0 GOTO 300
можно написать
ON SGN(X)+2 GOTO 100,200,300
- Чтобы комментарий к подпрограмме
не снижал быстродействия, его надо размещать в первых строках подпрограммы,
а вызывать подпрограмму обращением к строкам, следующим за комментарием. При
этом сколь угодно длинный комментарий не снизит быстродействия программы. Кроме
того, иногда можно построить подпрограмму таким образом, что, обращаясь к разным
строкам подпрограммы, можно заставить её выполнять несколько функций (универсальная
подпрограмма с несколькими точками входа. - Прим peg). Например:
1090 COLOR 0 1100 DRAW "U6D12U6E10G10F10H2U2D2L2BR2" 1110 COLOR 1 1120 RETURN
При вызове со строки 1100 подпрограмма рисует некоторую фигуру, а при обращении к строке 1090 - стирает её.
- В журнале неоднократно помещались программы, позволяющие при необходимости включать и выключать звук. А можно эту задачу решить проще - поставить выключатель последовательно с излучателем. Тогда можно будет отключать звук в любой программе независимо от того, предусмотрено в ней это или нет.
От редакции
О проблеме оптимизации программ (как по быстродействию, так и по занимаемому объёму памяти) сказано и написано уже немало. Но, с одной стороны, для многих читателей часть ранее опубликованных материалов может по каким-то причинам «оставаться за бортом», а с другой - эта тема, вообще говоря, неисчерпаема.
Относительно же необходимости оптимизации той или иной конкретной программы можно сказать следующее. Оптимизировать программу, затрачивая на это силы и время, имеет смысл лишь тогда, когда эту программу предполагается «выпускать в свет» или самому придётся пользоваться ею достаточно часто. Кроме того, оптимизация может потребоваться, если какая-либо очень нужная программа «чуть-чуть не влезает» в память машины В случае же, когда программа пишется «на один раз», тратить время и силы на её оптимизацию просто нерационально.